1. Relativité Restreinte et Espace Temps platIntroductionNous allons commencer par un tour
d'horizon sur la
RELATIVITÉ RESTREINTEet l'
ESPACE TEMPS plat associé : est
platun espace temps dont la métrique peut être mise sous une forme où les
coefficients ne dépendent pas des coordonnées. Cela va nous permettre de nous
rappeler l'objet de la RELATIVITÉ RESTREINTE et d'introduire les tenseurs et
tout ce qui tourne autour, concepts qui vont se révéler essentiels par la
suite, dans le contexte plus simple de la relativité Restreinte libre des
complications supplémentaires liées à la courbure de l'ESPACE
TEMPS . Dans cette partie nous allons exclusivement
travailler dans un espace temps plat et de plus en coordonnées orthonormées ( type coordonnées cartésiennes). Il est inutile de dire que
nous pourrions travailler dans n'importe quel système de coordonnées, mais ce
serait empiéter sur les parties suivantes, donc nous
différerons cet aspect.
Espace temps de la RR comparé à Espace et Temps de la
mécanique classiqueOn dit souvent que le RELATIVITÉ
RESTREINTE est une théorie de l'espace temps à 4 dimensions : trois d'espace,
une de temps. La mécanique Newtonienne utilise également trois dimensions
d'espace et une de temps, où est la différence ?
Si on considère un jardin,
variété à deux dimensions, nous allons repérer les points sur un tel plan en introduisant
arbitrairement des coordonnées, par exemple x, y orthogonales.
La
distance : invariant métrique classiqueIl est certain que ce qui va nous
intéresser ce sont les propriétés géométriques ( les
invariants) qui sont indépendantes des coordonnées arbitraires. Par exemple la distance entre
deux points donnée par :
Si on avait choisi un autre
système de coordonnées cartésiennes déduit du premier par une rotation des axes
x,y autour de l'origine, on aurait des
coordonnées x' et y' avec pour la
distance la même formule :
Nous en concluons que la distance
entre deux points est invariante vis à vis de tels changement de coordonnées.
C'est pourquoi il est important
de penser le plan comme variété à deux dimensions, bien que nous utilisions
deux nombres pour repérer les points. Ces nombres ne sont pas l'essence de la
géométrie, puisqu'ils se transforment en d'autres lorsqu'on fait subir une rotation
aux axes ( on peut les permuter) en laissant invariant
les distances, mais seulement un moyen conventionnel de la décrire. En
mécanique Newtonienne ce n'est pas le cas, on ne peut pas permuter l'axe du
temps avec un axe d'espace. Le temps est
une dimension indépendante de l'espace.
Construction d'un référentiel inertiel en RRIl en va autrement en RELATIVITÉ
RESTREINTE. Considérons les coordonnées (
t,x,y,z) de l'ESPACE TEMPS,
dans cet ordre. Les coordonnées spatiales (x,y,z) forment
un système cartésien standard, que l'on peut construire en assemblant des
barres rigides qui se coupent à angle droit. Ce système peut se mouvoir
librement non accéléré. La coordonnée temporelle peut être fournie par un jeu
d'horloges attachées aux barres. On peut supposer les barres infiniment longues
et les horloges infiniment nombreuses pour baliser tout l'espace temps ( expérience de pensée). Les horloges sont synchronisées en
considérant que si nous voyageons à une vitesse constante
v dans une direction d'un point A à un point B, la différence de temps marquée par les
horloges en A et B , va être la même que si j'effectue
le même voyage dans l'autre direction ( de B vers A) dans les mêmes conditions
( dans sa définition de l'article fondateur de la RELATIVITÉ RESTREINTE de
1905, Einstein utilise la lumière comme voyageur). Le système de coordonnées
ainsi construit est appelé
référentiel
inertiel ( ou Galiléen).
Evènements, points évènementsUn
événement ( on dit parfois point
événement) est défini par une occurrence dans l'espace et le temps, caractérisé
uniquement par (
t,
x,
y,
z).
Où les coïncidences sont fondamentalesEn fait Einstein insiste beaucoup
sur le concept de
coïncidence, seul
concept qui a une réalité physique selon lui, une
mesure d'espace temps correspond à une coïncidence entre :
- Le point événement
- Son image spatio
temporelle dans le référentiel : Les valeurs repérées sur les règles du point
du référentiel qui coïncide avec le point événement à l'instant considéré, la valeur de l'horloge
située en ce point à cet instant.
L'intervalle
d'espace tempsCeci étant précisé, introduisons
ex abrupto l'intervalle d'espace temps entre deux évènements.
Remarquons que cette expression
peut être positive, négative ou nulle ( même pour deux
points différents). Ici
c est un facteur constant correspondant
à une vitesse pour obtenir une équation homogène. Nous savons que c'est la
vitesse de la lumière, l'important pourtant n'étant pas que les photons
voyagent à la vitesse de la lumière mais qu'il y ait un invariant de ce type.
Cela signifie que si nous
procédons aux mêmes mesures dans un autre référentiel inertiel (
t',
x',
y',
z') nous allons obtenir la
même valeur de s²:
Espace de Minkowski C'est pourquoi , on peut affirmer
que la RELATIVITÉ RESTREINTE est une théorie se référant à un espace temps à 4 dimensions appelé
espace de Minkowski qui est un cas particulier
de variété à 4 dimensions dont nous parlerons plus tard. Comme nous allons le
voir, la transformation de coordonnées que nous avons implicitement définie
permet d'échanger les dimensions d'espace et de temps. Elle généralise la
notion d'invariance de la distance par rotation aux quatre dimensions. La
notion d'évènements simultanés perd sa signification absolue, le temps n'étant
plus absolu et dépendant du référentiel. La distinction entre temps et espace
qui sont liés par la relation (1.3) de l'espace de Minkowski est
conventionnelle et ceci bien que
l'espace et le temps gardent certaines caractéristiques propres, reflétées par
le signe différent dans (1.3)
La plupart des paradoxes de la RR
résultent de la persistance de la notion de temps absolu. En raisonnant en
Espace temps, la plupart de ces paradoxes disparaissent.
Coordonnées d'espace temps Introduisons une notation
adaptée. Les coordonnées d'espace temps seront dénotées par des lettres
affectées d'un index haut que nous appellerons "exposant" de type
lettre grecque représentant une valeur de 0 à 3, où 0 représente la coordonnée
"temps " soit :
Ne pas confondre cet
"exposant" avec un exposant mathématique. Pour simplifier nous
poserons également :
Ce qui permet d'éviter de
surcharger les formules. De ce fait, si nous gardons la seconde comme unité de
temps, l' unité de distance vaudra 3 × 10
8mètres. Si nous devons faire référence
aux dimensions d'espace seulement, nous utiliserons un exposant de type lettre
latine.
Comme nous allons souvent
l'utiliser, il va être commode d'écrire l'intervalle d'espace temps sous une
forme compacte.
La métrique
de MinkowskiNous allons introduire une matrice
4 x 4 ,
la
métrique, que nous écrirons avec deux index bas que nous appellerons
"indices" :
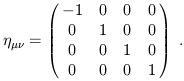
| (1. 
|
Un certain nombre d'ouvrages
utilisent une convention de signe opposée pour la métrique, donc soyons
prudents. Nous avons alors la formule sympathique suivante :
Remarquons que nous avons utilisé
la convention d'Einstein pour la sommation des index. Lorsqu'un index repéré
par la même lettre apparaît dans une telle formule en exposant et en indice,
cela signifie qu'on doit faire la somme
des produits des termes pour la même valeur de l'index, indexés de 0 à 3 dans
notre cas. Le résultat montre que (1.9) est identique à (1.3).
Considérons plus formellement les
types de transformation des coordonnées d'espace temps.
Quelle
sorte de transformation va laisser l'intervalle (1.9) invariant? Les translations : Où
am est un ensemble de quatre valeurs fixes. ( Remarquons que avons affecté le "prime" à
l'index pas à "x" ). Comme les translations laissent
 xm
xminvariant , il est évident que l'intervalle est
invariant.
Une transformation plus généraleUne transformation plus
générale consiste à multiplier le "quadri-vecteur colonne"
xmpar une matrice 4 x 4 indépendante de l'espace temps :
Soit en utilisant une
notation matricielle plus conventionnelle :
Ce type de transformation ne conserve pas les
différences
 xm
xm, mais les multiplient par la matrice

.
Quelles sortes de matrices laissent l'intervalle
invariant ? En respectant la notation propre
aux matrices cela implique que :
Car la transposée d'un produit de matrices est égal au
produit inversé des transposés et donc:
Déterminons les matrices
Lm'n qui satisfont à
(1.15) garantissant la
conservation de l'intervalle d'espace temps, lorsqu'on les utilise pour
transformer les coordonnées.
Groupe
de Lorentz Les matrices qui satisfont (1.14)
forment un groupe vis à vis de la multiplication appelé le groupe de Lorentz.
Il y a une relation étroite entre le groupe des rotations O (3) de l'espace
tridimensionnel et le groupe de Lorentz. Le groupe des rotations peut être
interprété comme le groupe des matrices 3 x 3 qui satisfont:
Où
1est la matrice Identité 3 × 3 . La similitude
avec (1.14) est évidente, la seule
différence résidant dans le signe
moins du premier terme de la métrique
h, représentant la coordonnée temporelle. Du coup, le
groupe de Lorentz est souvent référencé par O(3,1). La
matrice Identité 3 × 3 est simplement la
métrique de l'espace Euclidien 3D. Une métrique où toutes les valeurs sont
égales et positives est appelée
Euclidienne,
tandis que celles qui comme (1.

contiennent un seul signe moins sont appelées
Lorentziennes. Les transformations de Lorentz se divisent en
plusieurs classes. Rotations classiques La première est celle des
rotations classiques telles que la rotation dans le plan
x-
y :
L'angle de rotation

est une
variable périodique de période 2

.
Vitesse relatives : les propulsionsIl y a aussi des propulsions qui
peuvent s'interpréter comme des rotations entre l'espace et le temps. Un
exemple est donné ci dessous :
Le paramètre de propulsion
F à la différence des
rotations est défini de -

à +

. Il y a
aussi des transformations discrètes qui renversent la direction du temps ou
d'une ou plusieurs d'espace. Lorsque ces dernières sont exclues on a le groupe
propre de Lorentz SO(3,1). Une transformation générale
s'obtient en multipliant les transformations individuelles. L'expression
explicite pour cette matrice à 6 paramètres ( 3
rotations, 3 propulsions) est assez touffue et nous ne la donnerons pas ici. En
général les transformations du groupe de Lorentz ne vont pas commuter, le
groupe n'étant pas Abélien.
Le groupe de PoincaréL'ensemble qui inclut les
transformations de Lorentz et les quatre translations est le
groupe de Poincaré, non abélien, qui
comporte dix paramètres.
Nous ne serons pas surpris
d'apprendre que les propulsions correspondent aux changement
de coordonnées nécessitées lorsqu'on repère les évènements dans un nouveau
référentiel qui se meut à vitesse constante par rapport à l'original. Regardons
cela de plus près.
Transformation des coordonnéesPour la transformation décrite
par (1.18), les coordonnées transformées
t'et
x' sont données par :
Nous voyons que le point défini
par
x'= 0 se déplace . Sa vitesse est :
Avec une notation plus terre à
terre, en posant
F=
tanh
-1v, on obtient
où
g =
(1-v²)
-1/2. Notre
approche formelle rejoint l'approche conventionnelle pour établir les relation
de transformation de Lorentz.. L'application de ces
formules conduit à la dilatation du temps, à la contraction des longueurs etc.
Le
diagramme spatio temporel Le diagramme spatio
temporel se révèle être un outil très utile pour représenter l'espace de
Minkowski. Traditionnellement on ne représente que les variables
x et
t( une variable d'espace et la variable de temps) dans
un référentiel orthonormé. Remarquons que la représentation d'une seule
variable d'espace, parmi les trois, n'entache pas trop la généralité, du fait
que les trois variables d'espaces sont équivalentes et interchangeables.
Alors, selon (1.19), si on
représente l'axe x' dans le plan
x-
t, il est caractérisé par l'équation (
t' = 0). Il est fonction de la
propulsion et est décrit par
t =
xtanh
F,
tandis que l'axe
t' (
x' = 0) est décrit
par
t =
x/tanh
F. On
voit que les nouveaux axes (
x',y') d'espace
et de temps subissent une rotation qui les rapprochent l'un de l'autre sous
l'effet de la propulsion. Dans la représentation de ce diagramme, ils
n'apparaissent plus orthogonaux au sens Euclidien traditionnel
, bien que dans le contexte Lorentzien, qui
correspond à la "réalité physique" ils le restent. Ce n'est pas surprenant , car l'espace temps est à quatre dimensions et
sa représentation par une tranche 2D n'en est qu'une coupe qui ne le décrit
qu'imparfaitement.
Invariance du chemin de la lumière dans le diagramme.Il est instructif de considérer
le chemin suivi pour la vitesse
c = 1
dans les deux référentiels. Dans les coordonnées originales il est
décrit par
x = ±
t. Dans le nouveau système il est décrit par
x' = ±
t' qui correspond à la même droite que
x = ±
t.
La transformation laisse donc invariante dans ce diagramme les chemins de ce
type. Nous savons que
c est la
vitesse de la lumière, mais nous retrouvons par ce moyen le fait que la lumière
se déplace à la même vitesse dans les deux référentiels.
Les
cônes de lumièreL'ensemble des points qui est
relié à un événement unique par des droites correspondant au mouvement de la
lumière est appelé un cône de lumière. Ce cône de lumière est invariant par une
transformation de Lorentz. Les cônes de lumière sont divisés naturellement
entre passé et futur.
Les types d'intervallesLes points à l
'intérieur des cônes de lumière du
passé et du futur d'un point
p sont
dits
séparés par un intervalle de type
temps de
p alors que ceux à l'
extérieur sont dits
séparés par un intervalle de type espace de
p.
Ceux
sur le cône sont dits
séparés par un intervalle de type nul de
p où de
type lumière.En se référant à (1.3), nous voyons que l'intervalle de type
temps est négatif, celui de type espace positif et celui de type nul ( ou lumière) est nul. A noter que l'intervalle bien que
défini par un carré (
s²) peut être négatif, ce qui insiste sur
le fait que l'intervalle est bien
s²et pas
s.
Ceci met en lumière une
différence essentielle avec la théorie de Newton; si un point
q est séparé par un intervalle de type
espace du point
p, on ne sait pas
dire ( indépendamment du système de coordonnées) si
q est dans le futur, le passé
ou simultané à
p.
Vecteurs
en RRPour explorer plus avant la
structure de l'espace de Minkowski, il est nécessaire d'introduire les concepts
de vecteurs et de tenseurs. Commençons par les vecteurs qui nous sont plus
familiers.
Dans notre espace à quatre
dimensions les vecteurs auront quatre composantes, et souvent on les appelle
des quadri vecteurs. Ceci n'est pas neutre, par exemple il n'existe pas de
"
produit vectoriel " entre
deux quadri-vecteurs.
En plus de la dimension
, le point important à souligner
est que chaque vecteur est localisé à un certain point de l'espace temps. Nous
connaissons bien les vecteurs libres,
s'étendant d'un point de l'espace à un autre, que l'on peut translater ad libidum dans l'espace, et les vecteurs liés, s'étendant du point
p de l'espace à un autre point
q, avec une origine
p bien déterminée. Ces concepts ne sont pas utilisés en Relativité.
L'espace tangentA la place, nous associerons à
chaque point
p de l'espace temps,
l'ensemble de tous les vecteurs qui passent par ce point, que nous appellerons
l'espace tangent à
p , soit
Tp. Ce nom est inspiré par l'analogie à
l'ensemble des vecteurs passant par
pqui génèrent le plan tangent en
p à
une surface à deux dimensions courbée.
Mais inspiration mise à part,
l'important est que ces vecteurs soient localisés en un point et ne s'étendent
pas d'un point vers un autre ( même si pour des
raisons de commodité, nous ne nous priverons pas de les représenter sous forme
de flèche dans des diagrammes spatio temporels, la
direction est significative, mais la longueur représentant un autre paramètre
qu'une mesure de l'espace temps)
Plus tard nous ferons référence à
l'espace tangent à chaque point de quelque chose que nous construirons à partir
de l'espace temps. Pour l'instant, référons nous à
Tp comme à un espace vectoriel
défini en chaque point de l'espace temps.
Espace vectorielUn
espace vectoriel, rappelons le, est un ensemble d'objets ( vecteurs) qui peuvent être comparés, additionnés ( muni
d'une structure de groupe) et multipliés
par des nombres réels de façon linéaire.
Pour deux vecteurs quelconques
Vet
W et des nombres
a et
b nous avons :
Chaque espace vectoriel a une
origine ( vecteur nul) qui est l'élément neutre vis à
vis de l'addition vectorielle. Beaucoup d'espaces vectoriels possèdent aussi un
produit scalaire, qui est une fonctionnalité supplémentaire non indispensable.
Un vecteur est un objet géométrique parfaitement défini, comme un
champ de vecteurs qui est défini comme un ensemble de vecteurs tel qu'il y ait
un vecteur à chaque point de l'espace temps.
Faisceau tangentL'ensemble des espaces tangent
d'une variété M est appelée le
faisceau
tangent T(
M). Cependant, il est souvent utile dans
des configurations concrètes de décomposer les vecteurs en composantes
conformément à un ensemble de vecteurs
de base. Une base est un ensemble de vecteurs qui couvre tout l'espace
vectoriel ( chaque vecteur est une combinaison
linéaire des vecteurs de base) et qui sont linéairement indépendants les uns
des autres ( aucun n'est une combinaison linéaire des autres). Pour un espace
vectoriel donné, il y aune infinité des bases valides, mais chaque base va
comporter le même nombre de vecteurs, qui correspond à sa dimension. Pour un
espace tangent associé à un point dans l'espace de Minkowski, cette dimension
est évidemment quatre.
Supposons que pour chaque espace
tangent nous ayons établi une base constituée de 4 vecteurs ê
(m)avec
mÎ{0, 1, 2, 3} comme d'habitude.
Faisons correspondre la base aux coordonnées
xm,
Alors le vecteur de base ê
(1) va être porté par l'axe des
x, etc.. Même s'il n'est pas nécessaire
de choisir la base adaptée au système de coordonnées, c'est souvent bien pratique.
Nous pourrions être plus précis ici, mais comme ce point va être examiné plus
loin on peut se permettre de rester un peu vague. Chaque vecteur A va être
écrit comme une combinaison linéaire des vecteurs de base :
Composantes du vecteurLes coefficients
Amsont les
composantes du vecteur
A. La plupart du temps, on omet la base et on se réfère au vecteur "
Am",
mais gardons à l'esprit que c'est un raccourci. Le vecteur réel est un objet
géométrique, alors que les composantes ne sont que les coefficients des
vecteurs de base dans la base choisie. Comme nous omettons les vecteurs de
base, les index vont repérer les composantes des vecteurs et tenseurs. Nous
avons mis les index entre parenthèses pour les vecteurs de base pour rappeler
qu'il s'agit d'un ensemble de vecteurs et non pas des composantes d'un seul
vecteur.
Vecteur tangent Le vecteur tangent à une courbe
de l'espace temps est un exemple typique de vecteur. Une courbe ou un chemin
paramétré de l'espace temps est spécifié par ses coordonnées, fonction d'un
paramètre, par exemple
xm(

). Le vecteur tangent
V(

) a les
composantes :
Le vecteur lui même est défini
par
V =
Vm.ê
(m) Transformation des composantesUne transformation de Lorentz
change le coordonnées selon ( 1.11) mais laisse le
paramètre

en l'état, nous pouvons
donc en déduire que les composantes du vecteur tangent changent selon :
Mais le vecteur reste le même et
est donc invariant ( contrairement à ses composantes)
par la transformation de Lorentz.
Transformation des vecteurs de base Nous pouvons en déduire les
propriétés de la transformation des vecteurs de base. Appelons ê
(n') les vecteurs de bases les transformés de la
base initiale. Comme le vecteur est invariant nous avons
Cette relation doit être vérifiée
quelle que soit la valeur des composantes
Vµ .Nous pouvons
donc déduire :
On obtient la nouvelle base ê
(n') en multipliant l'ancienne base ê
(m)par l'inverse de la transformation de Lorentz
Ln'm. Mais l'inverse d'une transformation de
Lorentz est une transformation de Lorentz. On peut en adaptant la
notation, utiliser les même symboles
pour les deux matrices et aboutir à :
où
drm est le symbole de Kronecker
en quatre dimensions. ( Schutz
utilise une notation différente, en disposant toujours les indices en
configuration nord-ouest / sud-est), l'important est de suivre les index
primés. La règle de transformation pour les vecteurs de base s'obtient à partir
de (1.27)
Les vecteurs de base subissent la transformation de
Lorentz inverse de celle des composantes.Nous voyons que les vecteurs de
base subissent la transformation de Lorentz inverse de celle des composantes.
Résumons : Nous avons introduit
les coordonnées repérées par un exposant, qui se transforment d'une certaine
manière par la transformation de Lorentz. Ensuite nous avons considéré les
composantes d'un vecteur repérées également
par un exposant , ce qui est cohérent
puisqu'elles se transforment de la même manière par une transformation de
Lorentz. Dans un système fixe de coordonnées, chacune des quatre coordonnées
xmpeut être considérée comme une fonction dans l'espace temps, tout comme chacune
des composantes d'un champ de vecteurs. Les vecteurs de la base sur laquelle
s'appliquent les coordonnées se transforment de façon inverse et sont repérés
par un indice. Cette notation garantit que l'objet invariant construit par la sommation des vecteurs de
base multipliés par leurs composantes respectives soit inchangé par une
transformation ( on est parti de là). Fort de ces
acquis, nous allons essayer de généraliser cette règle à des objets à index
multiples ( tenseurs).
Espace
vectoriel dual A chaque espace vectoriel,
correspond un autre espace vectoriel, de même dimension, que nous allons définir
qui est appelé
espace vectoriel dual.
Espace cotangentL'espace vectoriel dual est en
général dénoté par un astérisque, et comme on appelle l'espace vectoriel
d'origine l'espace Tangent
Tp, le dual est appelé
l'espace cotangent dénoté
T*p.
L'espace dual est l'espace vectoriel de toutes les formes linéaires ( par des nombres réels) opérées sur l'espace vectoriel
original.
Forme linéaireEn jargon mathématique on dit que
si
 ÎTp*
ÎTp* est un
vecteur dual alors il est une forme linéaire qui satisfait à :
où
V,
W sont des vecteurs et
a,
b des nombres réels. La
propriété intéressante de ces formes linéaires est qu'elles ont une structure
d'espace vectoriel. Alors si

et
hsont
des vecteurs duaux nous avons :
Pour rendre cette formulation
plus concrète, introduisons un jeu de vecteurs duaux de base

définis par :
A partir de cette base duale, chaque
vecteur dual peut être défini par ses composantes, que nous repèrerons avec un
indice pour respecter la définition (1.33) :
L'analogie avec les vecteurs est
parfaite et comme pour eux, nous nous référerons aux vecteurs duaux, de façon abrégée
en mentionnant que leurs composantes

.
Vecteurs contravariants, vecteurs covariants Il faut mentionner que les
vecteurs de l'espace tangent
Tp ( que nous avons simplement appelés vecteurs) sont également
appelés
vecteurs contravariantset les vecteurs duaux de l'espace cotangent
vecteurs covariants. En fait personne ne s'offusquera si vous
désignez les vecteurs ordinaires ( ceux dont les
composantes ont un exposant) par le simple
terme "vecteur" et les autres par "vecteur dual".
Forme mono linéaire Un autre nom pour vecteur dual est forme mono linéaire , appelée ci après forme linéaire par défaut ( pour
les ordres supérieurs on spécifie, bilinéaire,.., multilinéaire) que nous
allons expliciter.
Action d'un vecteur dual sur un vecteurLa notation simplifiée par la
composante permet d'écrire simplement l'action d'un vecteur dual sur un vecteur
:
C'est pourquoi il est rarement
nécessaire d'inclure explicitement les vecteurs des bases. Les composantes
suffisent.
Les vecteurs sont les formes linéaires des vecteurs
duauxLa symétrie de la formule (1.35)
suggère que nous pouvons également considérer que les vecteurs sont les formes
linéaires des vecteurs duaux en définissant :
Donc espace vectoriel dual du
dual d'un espace vectoriel d'origine est l'espace vectoriel d'origine.

